2011-03-16
Tobias and Saalfeld found it a great idea to create this discussion page that, if ever possible, will be filled with the daily conceptual discussions and results. That way, all interested people can contribute and keep track on what we’re trying to tackle next.
We discussed the View concept:
Summary is that View\<T\> would be an interface that can return its target T, the data it is generated from:
public interface View<T> {
public T getTarget();
}
A View is an [...]Accessible that provides possibly transformed access to a subset of this target data.
Since we could not see any reasonable application for the bare View interface, we will not implement it but use it in informal speech about virtualized access. We will also use Target to refer to the underlying data.
Examples are IterableIntervalSubset, arbitrary Neighborhoods, RandomAccessibleView (formerly called View), RealRandomAccessibleView, TransformedRandomAccessibleView, StructuredElement, HyperShpere, SuperInterval…
We discussed the View concept (again) and Transforms:
We agreed that for Views that give transformed access it is more natural to specify the transform with respect to the underlying data. That is, the transform is applied to a coordinate in the data system to obtain a coordinate in the view system.
In matrix notation, a transform would look like y = Tx. Here, it is natural to refer to x as the source vector and to y as the target vector.
Applied to Views, we will therefore completely reverse our previous opinion and refer to the underlying data as the Source.
The View\<T\> interface would look like
public interface View<T> {
public T getSource();
}
For Transforms, we will adapt and simplify the CoordinateTransform and related interfaces from Fiji’s mpicbg submodule. There will be an integer and a real version as for Positionable and Localizable. Transform and RealTransform can specify the number of dimensions of its source and target domain. They look like
public interface Transform {
public int numSourceDimensions();
public int numTargetDimensions();
apply(long[] source, long[] target);
apply(Localizable source, Positionable target);
}
public interface RealTransform {
public int numSourceDimensions();
public int numTargetDimensions();
apply(double[] source, double[] target);
apply(RealLocalizable source, RealPositionable target);
}
The apply methods transfer source coordinates into target coordinates.
There will be an invertible version for each of these interfaces
public interface IvertibleTransform extends Transform {
applyInverse(long[] source, long[] target);
applyInverse(Positionable source, Localizable target);
InvertibleTransform inverse();
}
public interface IvertibleRealTransform extends RealTransform {
applyInverse(double[] source, source[] target);
applyInverse(RealPositionable source, RealLocalizable target);
InvertibleRealTransform inverse();
}
Note that target is transferred into source in that case.
We have extensively discussed the fact that for rendering a mapped image, an inverse transformation is required whereas one prefers to define transformations in the forward manner. Nevertheless, a view (renderer) should use the forward defined instance of a Transform to create its result with changes applied to that transform having a direct effect on the result (no creation of a fresh `inverse’). Other than in mpicbg, we will achieve this by implementing Renderers for forward transformations (those transformations that can be specified in one direction only will be defined as forward transformations). For invertible transformations, the Renderer will use a final Inverter that is a forward transformations that uses the inverse apply methods of an invertible transformation for its apply method.
How to proceed with the imglib2 namespace?
We think that it would be a great idea to be able to run both imglib and imglib2 together. This would relieve us from the need to port all the legacy imglib code into imglib2. Also, a shorter package hierarchy would be nice. With org.imglib2, we would match the Maven convention and the URL is still not registered…
Why not just call it org.imglib then? Wouldn’t clash with mpicbg.imglib of imglib1.
Because imglib.org is registered by somebody else already. Stephan Saalfeld 14:38, 24 March 2011 (CET)
2011-03-21
Efficient access for RandomAccessibleViews
I’ve been thinking all day about a reasonable concept for concatenation and simplification of Transforms for RandomAccessibleViews. No satisfying result so far, so at least I want to start writing down what it might look like in the end and what the problems are.
Simplifying View Transformations
The idea is that a view should always give you a RandomAccess that is as efficient as possible. When views are layered on top of each other it is often possible to combine and simplify their transformations.
Assume that we have a 90 degree rotated view A of an image I. and a 90 degree rotated view B of that view A. A RandomAccess on B could simply rotate by 90 degree and wrap a RandomAccess on A. The RandomAccess on A would in turn simply rotate by 90 degree and wrap a RandomAccess on I.
However, this would not a good idea for a hierarchy of many views. Instead, when we request a RandomAccess from B then we would like one that directly wraps a RandomAccess on I and rotates coordinates by 180 degree.
Transformable (leek)
Coincidentally, I was playing around with an idea for ROIs that might be applicable here. You’d like to be able to take a ROI in one space, apply a transform and get a ROI in the transformed space by transforming key internal coordinates. So that lead me to think of making ROIs implement “Transformable” if they wanted to. The some transformation could be applied to a transform itself - have a transform implement transformable so that its internal matrix could get re-jiggered to operate in the new space.
Here’s the interface that I was planning on implementing:
package mpicbg.imglib.transform;
/**
* @author leek
*
* A class is transformable if it can produce a copy of
* itself in the transformed space using the supplied transform.
*
* Note that a class may require either a Transform or an InvertibleTransform
* depending on whether the strategy is to transform coordinates in the
* source space into the destination space or to generate the object in
* the destination space by sampling invert-transformed points in the
* source space.
*
*/
public interface Transformable<O,T extends Transform> {
/**
* Generate a copy of the object in the transformed space.
* @param t the transform that maps points in the source space to those
* in the destination space.
* @return a copy built to operate similarly in the transformed space.
*/
public O transform(final T t);
}
You’d only want to implement Transformable in cases where the object has internal state which allows the transformed object to operate more efficiently than transformation of the object’s inputs, followed by application of the object’s function. For ROIs, the savings are clear - cost to transform a handful of vertices in a polygon versus cost of back-transforming millions of coordinates into the original space.
Now it obviously can be made to work for ROIs and it can be made to work to combine two linear transformations (dot product of matrices, right?). But other things are more complex and require more thought. At the end of it, each output is a function of the inputs and the trick is to composite a function that performs the operation. For a transform T1 to be transformable by transform T2, it seems that you need to combine and reduce an equation on the inputs of T1 for each of the outputs of T2. It’s a difficult enough problem that you might not want to make a transform generally transformable - you might want to have compositors with special knowledge regarding which classes can be combined to yield a new one and how it’s done.
Out-Of-Bounds Handling
In imglib2, out-of-bounds access is handled by ExtendedRandomAccessibleInterval If you have a RandomAccessibleInterval you can wrap it into an ExtendedRandomAccessibleInterval which extends to infinity. Like so:
F interval; // where F extends RandomAccessibleInterval< T >
OutOfBoundsFactory< T, F > factory = new OutOfBoundsMirrorFactory< T, F >( OutOfBoundsMirrorFactory.Boundary.SINGLE );
RandomAccessible< T > extended = new ExtendedRandomAccessibleInterval< T >( randomAccessible, factory );
ExtendedRandomAccessibleInterval is also a RandomAccessibleView. It might be inserted at any point in a view hierarchy. Here is an example:
Img< FloatType > img = LOCI.openLOCIFloatType(...);
RandomAccessibleView< FloatType > view1 = Views.extend( img );
RandomAccessibleIntervalView< FloatType > view2 = Views.superIntervalView( view1, new long[] {-20, -20}, new long[] {157, 157} );
RandomAccessibleView< FloatType > view3 = Views.extend( view2 );
RandomAccessibleIntervalView< FloatType > view4 = Views.superIntervalView( view3, new long[] {-100, -100}, new long[] {357, 357} );
The original img looks like this:
This is extended to infinity (using mirroring strategy) resulting in the unbounded RandomAccessible view1. A crop of view1 looks like this:
Then we take a subview view2 (which is again a bounded interval)
We extend that to get view3 and take a subview view4 which looks like this:
Now assume that we want RandomAccess into view4. If we know in advance interval in which we will use the access, view4 can possibly provide more efficient access. Consider this:
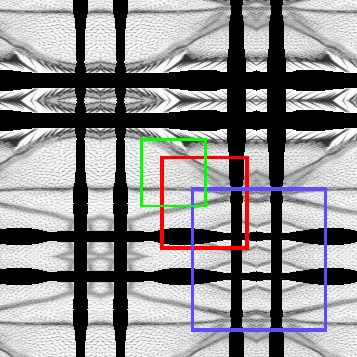
If we want to access only the green region, the RandomAccess can fall through all the way to the original img without needing out-of-bounds values. We simply wrap a RandomAccess on img with a coordinate translation to the top-left corner of view4
If we need to access the red region, we wrap a out-of-bounds RandomAccess on view1 (which wraps a RandomAccess on the img).
If we need to access the blue region, we wrap a out-of-bounds RandomAccess on view3 (which wraps a out-of-bounds RandomAccess on view1, which which wraps a RandomAccess on the img).
A view hierarchy may consist of an arbitrary sequence of views that do coordinate transforms and extending views. Depending on interval we want to access, sometimes the extending views “disappear”. In this case, transforms before and after the extending view can be concatenated and simplified if possible.
2011-03-24
Transformation Hierarchies
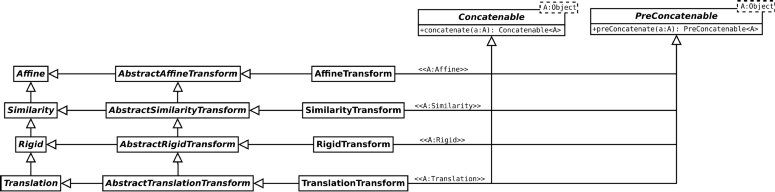Simplified visualization of the hierarchy of ImgLib2 transforms that can be reduced by concatenation. Note that the interfaces responsible for concatenation are not implemented by the transform hierarchy. Necessary access to trivial parameters in specialized transforms is implemented just once in abstract classes.
We thought that it might at some point be useful to have a generic way of contracting chains of transforms. The idea is to have a hierarchy of transformations, i.e., a Translation is a Rigid transform is an Affine transform, etc. The hierarchy determines which transformations can be concatenated. It would be hard to concatenate transformations from different branches in the tree. For example, it is possible to concatenate a Translation and a Rotation to a Rigid transform. However, it is not clear whether we always want to do that. So we decided that transforms should be concatenable with their descendants in the hierarchy but not the other way around. That is, a Rigid can be concatenated with a Translation (resulting in another Rigid). But a Translation can not be concatenated with a Rigid (because this would not always result in another Translation).
Having a generic way of concatenating Rigid with all of its children means that all children must also be a Rigid. That is, we must be able to ask a Translation for its rotation matrix and so on. I was afraid, that this adds too much (implementation) overhead, but Stephan convinced me that this is the best way to go. Actually, it should be possible to make this relatively painless by having an hierarchy of abstract transform classes.
We settled on the following scheme for implementing the transformation hierarchy:
There are interfaces Concatenable and PreConcatenable
public interface Concatenable< A >
{
public Concatenable< A > concatenate( A a );
public Class< A > getConcatenableClass();
}
if T implements Concatenable< A > that means I can concatenate it with an A, usually resulting in another T.
The hierarchy of transforms is implemented by a hierarchy of interfaces. However these interfaces do not implement Concatenable. Rigid cannot be Concatenable< Rigid > because this would mean that Translation (which extends Rigid) must be concatenable with Rigid (resulting in another Translation).
Instead, both the Rigid and Concatenable< Rigid > interfaces are implemented by the RigidTransform class
public class RigidTransform implements Rigid, Concatenable< Rigid >
{
@Override
public RigidTransform concatenate( Rigid a ) {...}
@Override
public Class< Rigid > getConcatenableClass()
{
return Rigid.class;
}
}
Similarly we have
public class TranslationTransform implements Translation, Concatenable< Translation >
{
@Override
public TranslationTransform concatenate( Translation a ) {...}
@Override
public Class< Translation > getConcatenableClass()
{
return Translation.class;
}
}
Note, that TranslationTransform cannot extend RigidTransform (because otherwise it would inherit Concatenable< Rigid >.)
We add an abstract class hierarchy between the interfaces and the transform classes. The abstract classes do not implement Concatenable, so at this level extension is still possible.
2011-03-25
Get and Set Strategy for different dimensionalities
If one wants to work with images that have different dimensionalities (e.g. 2d and 3d), it should be clearly defined how ImgLib handles Positionables, Localizables and location arrays.
getPosition calls: ImgLib will always iterate over the dimensionality of the Cursor which is queried for its position, i.e. one can always pass an array with a higher dimensionality and it will only set the lower dimensionality entries.
setPosition calls: ImgLib will always iterate over the dimensionality of the array that indicates the new location, i.e. one can pass an array or Localizable with a lower dimensionality and it will only set the new position in those lower dimensions.
For example 2d/3d:
Localizable2d.localize( array[3] ) - OK
Localizable3d.localize( array[2] ) - NOT OK
Positionable2d.setPostion( array[3] ) - NOT OK
Positionable3d.setPostion( array[2] ) - OK
We discussed this topic again and found that it is always bad practice to actually work with dimension vectors of different sizes. Instead, one should use views that map into a common n-space by either adding or removing a set of dimensions in one or both of the RandomAccessibles. Still, the behavior needs to be specified strictly. With an eye on efficiency and consistency, we revert our previous opinion to
Localizable2d.localize( array[3] ) - OK
Localizable3d.localize( array[2] ) - NOT OK
Positionable2d.setPostion( array[3] ) - OK
Positionable3d.setPostion( array[2] ) - NOT OK
Positionable2d.setPostion( Localizable3d ) - OK
Positionable3d.setPostion( Localizable2d ) - NOT OK
for the reason that in the latter case, the loop would require Localizable.numDimensions() to be called otherwise. There will be many situations where this cannot be inlined and thus be slower than using a temporary n in the executing class.
2011-05-02
We discussed the ExtendedRandomAccessibleInterval:
Tobias and Preibisch discussed today that the name ExtendedRandomAccessibleInterval is somehow irritating and also to long as it will be heavily used for OutOfBounds strategies.
It is irritating as it is actually NOT an Interval. Instead one could name it for example OutOfBoundsView, which is also much shorter. It is only used for this purpose and the name is self-explanatory.
We also added some convenience methods in the Views class to construct them very easily, see here: How does ImgLib2 handle OutOfBounds?
Should Iterator (and so Cursor) have a bck() call?
We have been discussing this several times with a two-folded answer:
- Yes, because iteration order for ImgLib2 Iterators is claimed to be constant. Given that, accessing the previous element (
bck()) call is always defined. - No, because it would require a substantial extension of the existing interfaces and classes. ImgLib2 Iterator could then implement ListIterator which is a lot of effort to implement.
In principal, I strongly support introducing it. It makes total sense but it is a change in the core. Stephan Saalfeld 17:03, 3 May 2011 (CEST)
I discussed it again with Tobias yesterday in detail and we came to the conclusion that it does not make too much sense. First of all, any Sampler can be copied at a certain location now, i.e. wait there. And it is also important to consider that going back would have a different logic than going forward as Cursors might crash when moved out. This means one would not be able to access +1, but one has to start at the last pixel of the e.g. Img<T>. That means when iterating back, the test has to be different: First get value, then move.
So maybe we just skip it? However, we could have an Interface that provides this functionality:
bck(); hasPrevious();
just for the case that somebody wants to implement it for some reason and does not has to do its own interface which would be incompatible with other people who would want to it. Could be named ReverseCursor or so… Stephan Preibisch 12:24, 4 May 2011 (CEST)
2011-05-04
Localizable and RealLocalizable Interface get()-methods
I noticed today that those two interfaces still have methods which are called getIntPostion(), getLongPosition() and so on which is different to the new naming scheme that is much better and shorter:
- numDimensions instead of `getNumDimensions()`
- localize instead of `getLocation()`
etc…
should we maybe change it as well to intPosition(), longPosition, etc?
Stephan Preibisch 12:24, 4 May 2011 (CEST)
Tobias pointed out that we should not as it is not clear if it is a getter or setter when passing an array.
2011-05-12
Positionables
Should we maybe have fast setPosition-calls for dimension 0?
In many algorithms we will need 1-dimensional Img<T>, like Histograms, Gauss and many more. A fast setPositionDim0(position) could be quite some speedup for arrays as
public void setPosition( final int pos, final int dim )
{
type.incIndex( ( pos - position[ dim ] ) * container.steps[ dim ] );
position[ dim ] = pos;
}
could simply become
public void setPositionDim0( final int pos )
{
type.incIndex( pos - position[ 0 ] );
position[ 0 ] = pos;
}
which saves a multiplication for many operations. It can also not be inlined by the JIT compiler as container.steps[ 0 ] cannot be made final, it could potentially always be changed…
The same applies for fwd(dim), bck(dim), move(dim), there a -- ++ and += can replace a array lookup…
Stephan Preibisch 12:27, 12 May 2011 (CEST)
What about having a 1D RandomAccess instead as we have done in PlanarImg for Cursor. That could implement the setPosition(long p, int d) method ignoring d. A 1D RandomAccess could, in addition, have the proposed method such that in situations where you know what you’re doing (read: where you can cast), you have a shorter call available. That approach would also relieve us from the need to implement that method in situations where it does not make sense at all, e.g. ShapeImg, that has no 1D.
Stephan Saalfeld 15:27, 12 May 2011 (CEST)
I like this way of realizing it, maybe we could also implement it on ImgFactory level. If a Img implements RandomAccessible1D, the factory could also have a special create( long size ) method (in e.g. RandomAccessible1DFactory) which returns for example <I extends ArrayImg<T,?> & RandomAccessible1D>, so no unchecked casts are necessary. Stephan Preibisch 16:15, 12 May 2011 (CEST)
2011-11-28
RealViews
Johannes pointed out that we will need to be able to handle images of different calibrations, e.g., compute the sum of two images with different pixel sizes.
I think, what we need to achieve this is something similar to what we have with the (integer) Views now. I will call them “RealViews” for now, and hope that someone comes up with a better name…
A RealView would implement (in analogy to the integer views)
public interface RealTransformedRealRandomAccessible< T > extends RealRandomAccessible< T >
{
/**
* @return the source {@link RealRandomAccessible}.
*/
public RealRandomAccessible< T > getSource();
/**
* @return transformation from view coordinates into {@link #getSource()
* source} coordinates.
*/
public RealTransform getTransformToSource();
}
Note, that RealTransform implementations do not yet exist. However the ideas are in place, see Transformation Hierarchies above. The interfaces to be implemented can be found in packages net.imglib2.concatenate and net.imglib2.transform.
Examples of implementation of the integer version of these interfaces can be found in net.imglib2.transform.integer (These are the ones I did for views).
Interpolated RealRandomAccessible
As the source for a RealView we need a RealRandomAccessible. This will be most likely a interpolated image. In net.imglib.interpolation we have InterpolatorFactories implementing nearest-neighbor and n-linear interpolation. What is left to do is write a (trivial) wrapper which turns a RandomAccessible into a RealRandomAccessible using an InterpolatorFactory. It would look more or less exactly like this:
public final class InterpolatedRandomAccessible< T > implements RealRandomAccessible< T >
{
private final RandomAccessible< T > source;
private final InterpolatorFactory< T, RandomAccessible< T > > factory;
public InterpolatedRandomAccessible( final RandomAccessible< T > source, final InterpolatorFactory< T, RandomAccessible< T > > factory )
{
this.source = source;
this.factory = factory;
}
@Override
public int numDimensions()
{
return source.numDimensions();
}
@Override
public RealRandomAccess< T > realRandomAccess()
{
return factory.create( source );
}
}
Using RealViews
Similar to what is now in Views there would be static methods to construct views, for example construct a RealView given a source RandomAccessible as well as source and target calibration.
One would wrap all of the source images into InterpolatedRandomAccessible and use RealViews as required to match the calibration of the target image. Then to carry out some operation, one would iterate through the target image and fetch the (possibly interpolated) values from the corresponding locations in the respective source views.
2012-01-28
We have discussed with Tobias that two additional integer views would be very helpful:
- Joining multiple images of the same size and dimensions into one or more dimensions of a single image (composition as opposed to decomposition which is implemented by hyperslice views).
- Adding a new dimension considering an existing dimension as interleaved data.
When done properly this has the potential to replace or at least simplify PlanarImg like containers since they could be expressed as a composition of multiple ArrayImg-s. Stephan Saalfeld 16:11, 18 January 2012 (CET)
2012-11-21
Another useful integer view comes to mind:
- Stack two images with all dimensions d < n-1 in the (n-1)th dimension. That would enable to load an image piecewise or to grow a time sequence etc.
The stack view is a special form of a `composite’ view (do not confuse with dimensional composition as mentioned above—clarify terminology!) that consists of two RandomAccessible<T> or RandomAccessibleInterval<T> that combine their values following some composition rule. Examples:
- a stack of images
- two images overlaid on top of each other
- an image that includes another image at a specified location
…
For those that are familiar with it, AWT has the Composite interface to specify the pixel operation for combining two rasters (such as copy, add, multiply, alpha, etc.). TrakEM2 is another good example from the Fiji universe. It represents 3D images that are a stack of 2D images that are composites of transformed 2D images or 2D projections of 3D images.
For ImgLib2, we could have the composition principle generalized and provide some special purpose implementations (stacking, AWT raster composition, TrakEM2-alike images).
