TrackMate Performance
This is a very incomplete DRAFT
Contents
- 1 The test machine
- 2 Time of execution.
- 2.1 The DoG & LoG detectors.
- 2.1.1 Processing time for a 2D image as a function of its size.
- 2.1.2 Processing time for a 3D image as a function of its size.
- 2.1.3 Processing time for a 2D image as a function of the spot radius.
- 2.1.4 Processing time for a 3D image as a function of the spot radius.
- 2.1.5 Choosing between DoG and LoG based on performance
- 2.1 The DoG & LoG detectors.
The test machine
The computer used for these tests is the following:
Mac¬Pro mi-2010 Processor 2 x 2.66 GHz 6-Core Intel Xeon Memory 24 GB 1333 MHz DDR3 ECC Software Mac OS X Lion 10.7.5 (11G63)
Time of execution.
The tests reported here were run on an Apple MacPro, 2 x 2.66 GHz 6-Core Intel Xeon, 24 Go 1333 MHz DDR3, running Mac OS X v10.7.5, with Java 1.6. The detectors instantiated were tamed to use only 1 thread. Unless indicated, the median filter and the sub-pixel localization were not done.
The DoG & LoG detectors.
Processing time for a 2D image as a function of its size.
For a uint16 image, varying its size, containing 200 gaussian spots of radius 3 (everything is in pixel units).
| N (pixels) | Image size | DoG detector time (ms) | LoG detector time (ms) |
|---|---|---|---|
| 256 | 16x16 | 3.0 | 4.8 |
| 1024 | 32x32 | 2.95 | 4.3 |
| 4096 | 64x64 | 3.95 | 4.35 |
| 16384 | 128x128 | 7.9 | 5.85 |
| 65536 | 256x256 | 23.35 | 17.7 |
| 262144 | 512x512 | 88.2 | 61.15 |
| 1048576 | 1024x1024 | 357.3 | 251.65 |
| 2359296 | 1536x1536 | 789.85 | 605.4 |
| 4194304 | 2048x2048 | 1463.4 | 1201.1 |
For the DoG detector, unsurprisingly, we find that the execution time is proportional to the number of pixels, following approximately t (ms) = 3.4e-4 x Npixels. This is expected as all calculations are done in direct space.
The LoG detector operates in Fourier space, and because of the Fourier transform implementation we use, the images are padded with 0s to reach a size equal to a power of 2. This does not show here as all but one tests are made with such a size. Still, the execution time slightly deviates from the linear case, and shows a slight quadratic shape. The best linear fit yields a low in t (ms) = 2.8e-4 x Npixels, showing that the LoG detector is slightly quicker than the DoG detector.
Processing time for a 3D image as a function of its size.
| N (pixels) | Image size | DoG detector time (ms) | LoG detector time (ms) | |
|---|---|---|---|---|
| 4096 | 16x16x16 | 8.7 | 24.7 | |
| 32768 | 32x32x32 | 23.5 | 38.5 | |
| 262144 | 64x64x64 | 129.3 | 159.2 | |
| 2097152 | 128x128x128 | 875.1 | 936.3 | |
| 16777216 | 256x256x256 | 7054.0 | 7462.4 | |
| 134217728 | 512x512x512 | 61477.2 | 58860.6 |
And again, the processing time is found to be linear with the number of pixels. The linear fit is slightly steeper, however: t (ms) = 4.6e-4 x Npixels, which we attribute to the 3D kernel overhead.
Interestingly, the LoG detector seems to become the slowest at intermediate size, which I cannot interpret well.
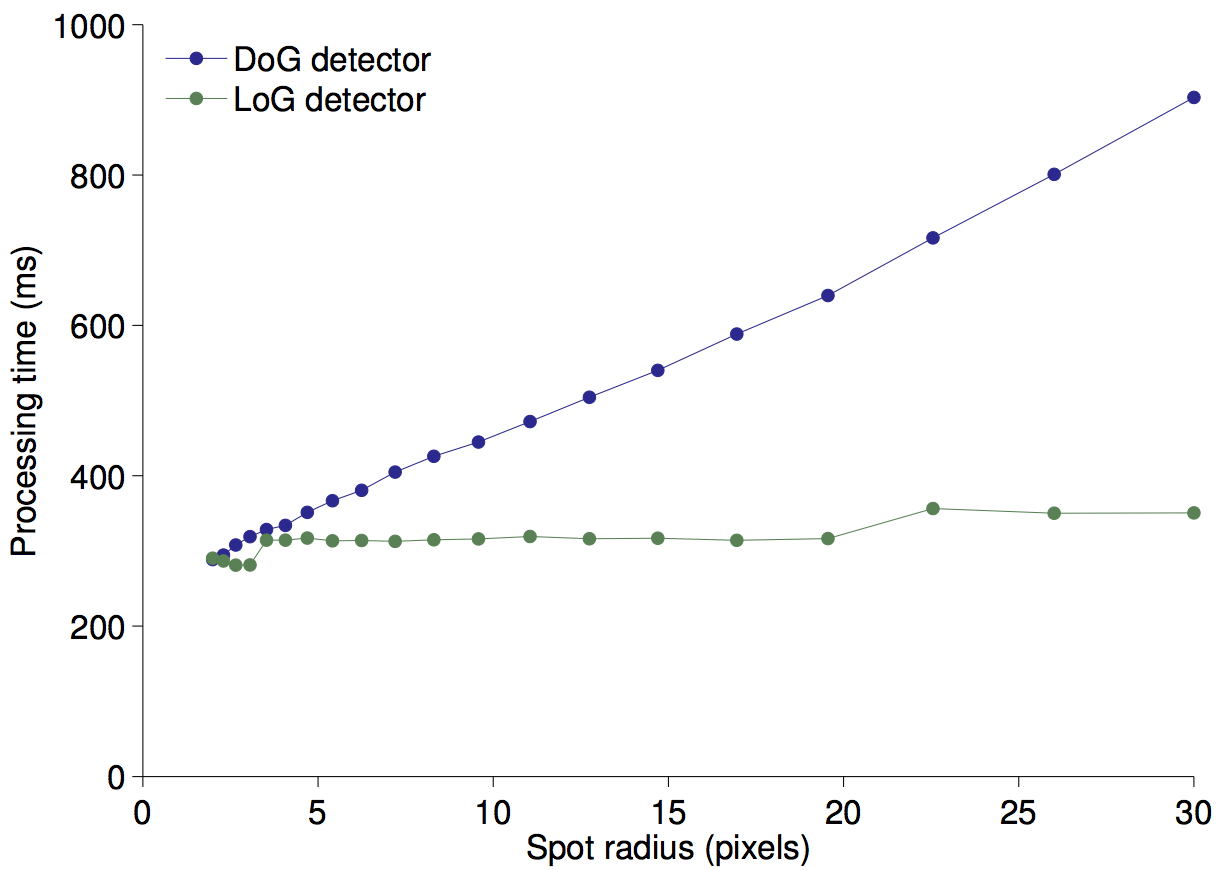
Processing time for a 2D image as a function of the spot radius.
We used a 1024x1024 uint16 image, with 200 gaussian spots, the size of which we varied. The detector was tuned to this radius.
We find that for the DoG detector, the processing time to increase linearly with the specified radius, following approximately t (ms) = 20.5 x radius + 260. As the difference-of-gaussians is calculated in the direct space, a marked increase is expected as there is more pixels to iterate over. Without optimization, we should however have found the time to be increasing with the square of the radius, and find the same dependence that for the image size. Thanks to the clever implementation of gaussian filtering[1], this is avoided.
The LoG detector shows a near-constant processing time, which makes it desirable for spots larger than 2 pixels in radius. This is due to the way we compute the convolution which is explained below.
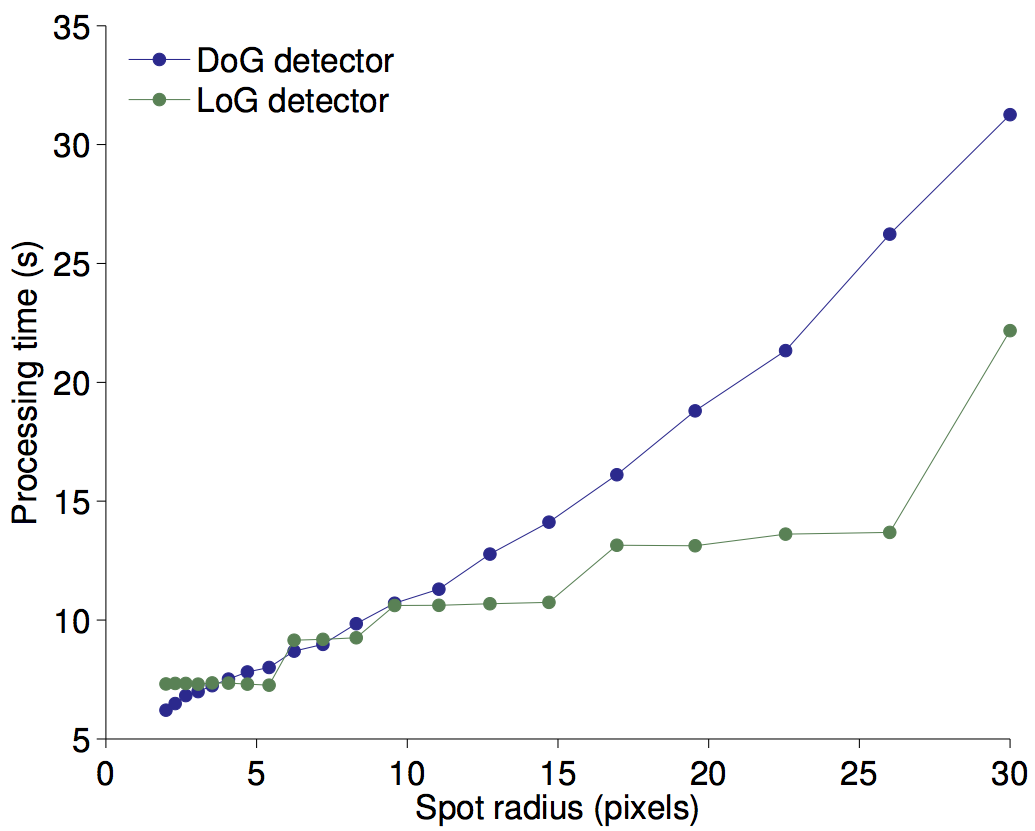
Processing time for a 3D image as a function of the spot radius.
This time we used a 256x256x256 3D image, but with otherwise the same parameters.
The processing time increases, but this time deviates slightly from linearity in the DoG case. We retrieve the 3D kernel overhead we had for the 3D images.
The LoG performance clearly highlights the 0-padding used because of the Fourier transform: Indeed, the processing time increase in a step-wise manner. We use the Fourier transform to compute the convolution by the LoG kernel. But for the implementation we use, the kernel image (and the source image as well) are padded by 0 until their size reaches a power of 2 (128, 256, 512, etc...). Whenever the required kernel size is smaller than this power of 2, its size is increased to this value. Because ultimately the processing time depends on the number of pixels, we see a constant processing time until the kernel size imposes a larger power of 2.
Choosing between DoG and LoG based on performance
This stepwise evolution makes it slightly harder to choose between LoG and DoG detectors based on performance. As a crude rule of thumb we will remember that
- The LoG detector outperforms the DoG detector in 2D for radiuses larger than 2 pixels.
- The LoG detector outperforms the DoG detector in 3D for radiuses larger than 4 pixels.